Como serei monitor da turma de 2011 de Geometria Analítica e Álgebra Linear da FCA, começo nesse fim de dezembro a escrever, sem muito rigor, sobre tópicos da matéria. Faço isso por dois motivos. Primeiro, o rigor em excesso no início pode ser prejudicial e até afugentador, por isso, um texto informal ajuda na compreensão geral do assunto. Segundo, pretendo melhorar o blog como ferramenta de auxilio da monitoria, assim, preciso seguir minimamente os tópicos da ementa e assim farei de modo descontraído, pois os formalismos estão nos livros.
Se o início da disciplina não for feito em cima de matrizes e sistemas lineares, então possívelmente será feito sobre vetores.
Nosso primeiro contato com vetores acontece geralmente no ensino médio, e é feito de maneira a familiarizar o aluno com as operações básicas. Uma breve retrospectiva:
(1) Define-se vetor como sendo um segmento de reta orientado, mas essa não é uma definição interessante e veremos o por quê mais adiante.
(2) Representamos algebricamente os vetores no plano como sendo duplas de números. Se os vetores partem da origem, então a dupla $(x,y)$ representa o "segmento de reta" que sai origem e chega até o ponto $(x,y)$. Mais geral, dado um ponto inicial $P_0=(a,b)$ e um ponto final $P=(c,d)$, temos $\vec{P_0P}=(c-a,d-b)$ o vetor que liga $P_0$ a $P$.
(3) A soma vetorial é feita componente a componente. Se $\vec{v_1}=(x_1,y_1)$ e $\vec{v_2}=(x_2,y_2)$ são vetores, então a soma fica $\vec{v_1}+\vec{v_2}=(x_1+x_2,y_1+y_2)$. A subtração é vista como a soma de vetores, mas o vetor que subtraí fica com o sinal contrário:
Os vetores obedecem aos axiomas de espaço vetoriais, coisa que podemos falar mais adiante. Basicamente, a soma é comutativa e associativa, existe inverso aditivo, elementro neutro da adição, e etc etc etc...
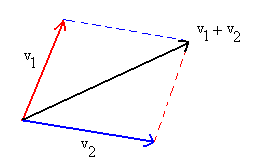
(4) Graficamente, a soma vetorial é feita pela regra do paralelogramo.
(5) Muitas vezes precisamos determinar o tamanho do vetor. A visualização gráfica do vetor no plano sugere naturalmente que o comprimento do vetor venha do teorema de Pitágoras. Ou seja, chamamos de módulo de $\vec{v}$, $||\vec{v}||$, o comprimento do vetor v, cuja expressão é $||\vec{v}||=\sqrt{x_1^2+y_1^2}$.
(6) Não existe "divisão" vetorial, mas existe multiplicação de um vetor por um escalar: $k\vec{v}=k(x_1,y_1)=(kx_1,ky_1)$ com $k\in\mathbb{R}$. Se $k=\dfrac{1}{||\vec{v}||}$, então $k\vec{v}=\dfrac{\vec{v}}{||\vec{v}||}=\vec{u}$ e dizemos que u é vetor unitário. O que acabamos de fazer foi dividir cada componente de $\vec{v}=(x_1,y_1)$ pelo tamanho do vetor, assim, geramos um novo vetor $\vec{u}$, cuja direção é a mesma de $\vec{v}$, mas seu comprimento é menor que o original e tem tamanho 1.
(7) O produto escalar (ou produto interno) é uma operação entre dois vetores que a eles associa um número, Normalmente se $\vec{v_1}=(x_1,y_1)$ e $\vec{v_2}=(x_2,y_2)$, então $\vec{v_1}\cdot\vec{v_2}=x_1x_2+y_1y_2$. Digo normalmente pois existem outros tipos de produtos internos, mas isso falaremos depois.
O produto vetorial é outro tipo de operação entre dois vetores e que a eles associa um novo vetor, ortogonal aos dois primeiros. Dedicarei um post especial para estudar o produto escalar e o vetorial, explicar algumas propriedades e principalmente aplicações na física.
Bem, se os vetores são os mesmos que estudamos no colégio, qual a diferença para os vetores de agora?
(i) Os vetores agora são fundamentados dentro de um assunto maior, que é a álgebra linear. A álgebra linear se ocupa basicamente das transformações lineares, que podem ser vistas como funções entre espaços vetoriais. Essas coisas farão mais sentido no futuro, quando as estudaremos mais a fundo, etc. Uma aplicação dos conceitos está, por exemplo, nos sistemas lineares $Ax=b$, quando dizemos que é necessário e suficiente que b pertença à imagem da transformação linear A para que exista solução.
(ii) Na realidade, a álgebra linear é uma disciplina separada da geometria analítica, mas num curso introdutório é interessante associá-las pois a geometria ajuda a entender os conceitos da álgebra, assim como a álgebra vetorial vai facilitar muito alguns problemas de geometria.
(iii) Uma outra coisa muito interessante que a álgebra linear permite é generalizar o conceito de dimensão. No plano, um vetor é dado por uma dupla de números. No espaço, uma tripla. Em 4 dimensões, são necessários 4 números, ou uma quádrupla, para determinar o vetor, e assim seguem as outras definições (de produto interno, módulo, etc). Isso não significa que essas dimensões existam fisicamente, mas elas fazem sentido matematicamente.
(iv) A palavra vetor vem do latim vector - aquele que transporta alguma coisa. O significado etimológico não se relaciona com a definição de "segmento de reta orientado", porém, é mais intuitivo pensar em vetores como transportadores de pontos, como a definição da palavra sugere. Mas como assim?
Bem, imagine um mapa cartográfico - vamos pegar dois pontos nesses mapa, $P_0=(x_1,y_1)$ e $P=(x_2,y_2)$. Suponha que estejamos dentro de um carro em $P_0$ e nosso destino é chegar em $P$. Sabemos, como eu expliquei acima, que um vetor age sobre os pontos, transportando-os. Vamos empregar esta idéia em nossa situação: O vetor que liga $P_0$ a $P$ é dado por $\overline{P_0P}=P-P_0=(x_2-x_1,y_2-y_1)$. Se somármos esse vetor com o nosso ponto inicial, $\overline{P_0P} + P_0$, vamos obter: $(x_2-x_1+x_1,y_2-y_1+y_1) = (x_2,y_2) = P$, uma vez que $\overline{P_0P} + P_0=P-P_0+P_0=P$ ou seja, bastaria nos deslocarmos $||\overline{P_0P}||$ unidades de comprimento na direção de $\overline{P_0P}$ para que chegássemos ao ponto $P$. Então repare que de fato os vetores representam deslocamentos de um ponto até outro quando efetuamos essa soma.
Ano que vem começo a falar da parametrização de reta e de outras coisas, utilizando a ideia acima. Também estou devendo um post sobre Taylor em duas variáveis, o que farei provavelmente em fevereiro. Abraços!
Se o início da disciplina não for feito em cima de matrizes e sistemas lineares, então possívelmente será feito sobre vetores.
Nosso primeiro contato com vetores acontece geralmente no ensino médio, e é feito de maneira a familiarizar o aluno com as operações básicas. Uma breve retrospectiva:
(1) Define-se vetor como sendo um segmento de reta orientado, mas essa não é uma definição interessante e veremos o por quê mais adiante.
(2) Representamos algebricamente os vetores no plano como sendo duplas de números. Se os vetores partem da origem, então a dupla $(x,y)$ representa o "segmento de reta" que sai origem e chega até o ponto $(x,y)$. Mais geral, dado um ponto inicial $P_0=(a,b)$ e um ponto final $P=(c,d)$, temos $\vec{P_0P}=(c-a,d-b)$ o vetor que liga $P_0$ a $P$.
(3) A soma vetorial é feita componente a componente. Se $\vec{v_1}=(x_1,y_1)$ e $\vec{v_2}=(x_2,y_2)$ são vetores, então a soma fica $\vec{v_1}+\vec{v_2}=(x_1+x_2,y_1+y_2)$. A subtração é vista como a soma de vetores, mas o vetor que subtraí fica com o sinal contrário:
$\vec{v_1}-\vec{v_2}=\vec{v_1}+(-\vec{v_2})=(x_1-x_2,y_1-y_2)$.
Os vetores obedecem aos axiomas de espaço vetoriais, coisa que podemos falar mais adiante. Basicamente, a soma é comutativa e associativa, existe inverso aditivo, elementro neutro da adição, e etc etc etc...
(4) Graficamente, a soma vetorial é feita pela regra do paralelogramo.
(5) Muitas vezes precisamos determinar o tamanho do vetor. A visualização gráfica do vetor no plano sugere naturalmente que o comprimento do vetor venha do teorema de Pitágoras. Ou seja, chamamos de módulo de $\vec{v}$, $||\vec{v}||$, o comprimento do vetor v, cuja expressão é $||\vec{v}||=\sqrt{x_1^2+y_1^2}$.
(6) Não existe "divisão" vetorial, mas existe multiplicação de um vetor por um escalar: $k\vec{v}=k(x_1,y_1)=(kx_1,ky_1)$ com $k\in\mathbb{R}$. Se $k=\dfrac{1}{||\vec{v}||}$, então $k\vec{v}=\dfrac{\vec{v}}{||\vec{v}||}=\vec{u}$ e dizemos que u é vetor unitário. O que acabamos de fazer foi dividir cada componente de $\vec{v}=(x_1,y_1)$ pelo tamanho do vetor, assim, geramos um novo vetor $\vec{u}$, cuja direção é a mesma de $\vec{v}$, mas seu comprimento é menor que o original e tem tamanho 1.
(7) O produto escalar (ou produto interno) é uma operação entre dois vetores que a eles associa um número, Normalmente se $\vec{v_1}=(x_1,y_1)$ e $\vec{v_2}=(x_2,y_2)$, então $\vec{v_1}\cdot\vec{v_2}=x_1x_2+y_1y_2$. Digo normalmente pois existem outros tipos de produtos internos, mas isso falaremos depois.
O produto vetorial é outro tipo de operação entre dois vetores e que a eles associa um novo vetor, ortogonal aos dois primeiros. Dedicarei um post especial para estudar o produto escalar e o vetorial, explicar algumas propriedades e principalmente aplicações na física.
Bem, se os vetores são os mesmos que estudamos no colégio, qual a diferença para os vetores de agora?
(i) Os vetores agora são fundamentados dentro de um assunto maior, que é a álgebra linear. A álgebra linear se ocupa basicamente das transformações lineares, que podem ser vistas como funções entre espaços vetoriais. Essas coisas farão mais sentido no futuro, quando as estudaremos mais a fundo, etc. Uma aplicação dos conceitos está, por exemplo, nos sistemas lineares $Ax=b$, quando dizemos que é necessário e suficiente que b pertença à imagem da transformação linear A para que exista solução.
(ii) Na realidade, a álgebra linear é uma disciplina separada da geometria analítica, mas num curso introdutório é interessante associá-las pois a geometria ajuda a entender os conceitos da álgebra, assim como a álgebra vetorial vai facilitar muito alguns problemas de geometria.
(iii) Uma outra coisa muito interessante que a álgebra linear permite é generalizar o conceito de dimensão. No plano, um vetor é dado por uma dupla de números. No espaço, uma tripla. Em 4 dimensões, são necessários 4 números, ou uma quádrupla, para determinar o vetor, e assim seguem as outras definições (de produto interno, módulo, etc). Isso não significa que essas dimensões existam fisicamente, mas elas fazem sentido matematicamente.
(iv) A palavra vetor vem do latim vector - aquele que transporta alguma coisa. O significado etimológico não se relaciona com a definição de "segmento de reta orientado", porém, é mais intuitivo pensar em vetores como transportadores de pontos, como a definição da palavra sugere. Mas como assim?
Bem, imagine um mapa cartográfico - vamos pegar dois pontos nesses mapa, $P_0=(x_1,y_1)$ e $P=(x_2,y_2)$. Suponha que estejamos dentro de um carro em $P_0$ e nosso destino é chegar em $P$. Sabemos, como eu expliquei acima, que um vetor age sobre os pontos, transportando-os. Vamos empregar esta idéia em nossa situação: O vetor que liga $P_0$ a $P$ é dado por $\overline{P_0P}=P-P_0=(x_2-x_1,y_2-y_1)$. Se somármos esse vetor com o nosso ponto inicial, $\overline{P_0P} + P_0$, vamos obter: $(x_2-x_1+x_1,y_2-y_1+y_1) = (x_2,y_2) = P$, uma vez que $\overline{P_0P} + P_0=P-P_0+P_0=P$ ou seja, bastaria nos deslocarmos $||\overline{P_0P}||$ unidades de comprimento na direção de $\overline{P_0P}$ para que chegássemos ao ponto $P$. Então repare que de fato os vetores representam deslocamentos de um ponto até outro quando efetuamos essa soma.
Ano que vem começo a falar da parametrização de reta e de outras coisas, utilizando a ideia acima. Também estou devendo um post sobre Taylor em duas variáveis, o que farei provavelmente em fevereiro. Abraços!






Nenhum comentário:
Postar um comentário